O_SESSAME::RungeKuttaIntegrator Class Reference
[Integration Library]

#include <RungeKuttaIntegrator.h>

Inheritance diagram for O_SESSAME::RungeKuttaIntegrator:

[legend]List of all members.

---

Detailed Description

Implementation of a Runge-Kutta (Fourth Order) Integrator.

This class defines the functions that are required for all Integrator types (ie

See also:

RungeKuttaIntegrator,

AdamsBashfourthIntegrator, etc).

Integration in the Open-Sessame Framework is modeled after integration in MatLab. To integrate, a user must specify a Right-Hand Side (RHS) function that has the form , where is the time (in seconds), is the vector of states being integrated, 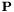is a matrix of constants, and is a reference to an external function which can be used to evaluate other parameters necessary for the RHS equation. The integration strategy will then evaluate the function 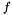at various timesteps, depending on the integration algorithm, and combine the results together to approximate the integrated solution.

Integration is specifically useful in the Open-Sessame Framework for numerically evaluating the equations of motion (EOM) of a spacecraft. The attitude & orbit EOM are usually defined as the time rate of change of the states (rotations, angular velocities, position, angular momentum, energy, etc) which can be integrated to determine the state of the spacecraft at some future time. For example, to evaluate the quaternion at some time :

testAttitudeIntegration.cpp testOrbitIntegration.cpp

Todo:

document algorithm testAttitudeIntegration.cpp testOrbitIntegration.cpp

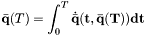
Definition at line 28 of file RungeKuttaIntegrator.h.

Public Member Functions
	RungeKuttaIntegrator ()
	Creates a default, unitialized RK-integrator.
Matrix	Integrate (const vector< ssfTime > &_propTime, odeFunctor _odeFunctorPtr, const Vector &_initialConditions, Orbit *_Orbit, Attitude *_Attitude, const Matrix &_constants, const Functor &_functorPtr)
	Integrates the Right-Hand Side (RHS) equation using a Runge-Kutta 4th Order integrator.
void	SetNumSteps (const int &_numSteps)
	Set the number of integration steps.
int	GetNumSteps ()
	Return the number of integration steps.
Private Attributes
int	m_NumSteps
	number of integration steps performed b/w every timestep

---

Constructor & Destructor Documentation

O_SESSAME::RungeKuttaIntegrator::RungeKuttaIntegrator (   )

Creates a default, unitialized RK-integrator. Definition at line 18 of file RungeKuttaIntegrator.cpp.

---

Member Function Documentation

Matrix O_SESSAME::RungeKuttaIntegrator::Integrate (  const vector< ssfTime > &  _propTime, odeFunctor  _odeFunctorPtr, const Vector &  _initialConditions, Orbit *  _Orbit, Attitude *  _Attitude, const Matrix &  _constants, const Functor &  _functorPtr )  [virtual]

Integrates the Right-Hand Side (RHS) equation using a Runge-Kutta 4th Order integrator. This function will integrate an equation of the form from to given initial conditions, an orbit and attitude object (or empty references if not required), a matrix of constants, and an external call-back function. Parameters: _propTime  This input variable specifies the list of integration times, from the starting value (first time) to the ending integration (last time) with the specified intervals. If no specific intervals are required (and can be interpolated later), the user needs to just specify the beginning and end times of integration. This vector is built by creating ssfTime object, and "push_back" them onto the vector list: vector<ssfTime> integrationTimes; ssfTime begin(0); ssfTime end(begin + 20); integrationTimes.push_back(begin); integrationTimes.push_back(end); _FunctorPtr  This is the reference (odeFunctor) to the Right-Hand side (RHS) of the integration equation. It should be a single function that computes the time derivative of the state given the time, current state, and other parameters. _initialConditions  The vector of initial conditions of the state being integrated. It can be any sized. _pOrbit  This is a pointer to an Orbit object. It will be passed directly to the RHS and may be used for evaluating the dynamics or disturbance torque/forces. However, if no orbit is required, or used, the user should only pass a NULL pointer and the orbit object shouldn't be used in the user's RHS function. _pAttitude  This is a pointer to an Attitude object. It behaves much the same way as _Orbit above. It will be passed directly to the RHS function for use in evaluation, but if not used, the user should only pass a NULL pointer, and the attitude object not used in the RHS function. _constants  This is a matrix of constants that is required by the RHS function. The constants are passed to each evaluation of the RHS, and may be any size, and store any values the user requires. Examples include Moments of Inertia, ballistic coefficients, mass, etc. _functorPtr  The Functor is a call-back function that the RHS can use to evaluate an external function call. The prototype of the _functorPtr must correspond to the Functor definition, but other than that, may perform any calculations required by the user in the RHS function. Returns: The output of the integration function is a matrix of calculated integration times (meshpoints), and integrated state values at each of the meshpoints. where /f$t_T/f$ is the time at step T, and /f$x_{i,T}/f$ is the state value of element i, at time step T. Implements O_SESSAME::Integrator. Definition at line 107 of file RungeKuttaIntegrator.cpp.

void O_SESSAME::RungeKuttaIntegrator::SetNumSteps (  const int &  _numSteps  )

Set the number of integration steps. Parameters: _numSteps  number of steps to include between integration timesteps Definition at line 41 of file RungeKuttaIntegrator.h.

int O_SESSAME::RungeKuttaIntegrator::GetNumSteps (   )

Return the number of integration steps. Returns: current number of integration steps performed b/w every timestep Definition at line 46 of file RungeKuttaIntegrator.h.

---

Member Data Documentation

int O_SESSAME::RungeKuttaIntegrator::m_NumSteps [private]

number of integration steps performed b/w every timestep Definition at line 48 of file RungeKuttaIntegrator.h.

---