Table of Contents : Introduction to the Open-Sessame Framework : Tutorials
Rotation Tutorial Answer
Quaternion myQuat(0.5, 0.5, 0.5, 0.5);
cout << myQuat;
cout << myQuat.GetMRP();
DirectionCosineMatrix myDCM(10*RPD, -30*RPD, 150*RPD, 321);
Rotation myRot1(myQuat);
Rotation myRot2(myDCM);
cout << (myRot1 * myRot2).GetDCM();
Matrix Answer(3,3);
Back to: Rotation Tutorials
Utility Tutorial Answer
- Create an ssfTime object, set the epoch to the current real time, and the stored 'current' time to 50 seconds later. Output both of these in DateTime and JulianDate format to the console.
ssfTime myTime;
myTime.SetEpoch(Now());
myTime.Set(myTime.GetEpoch() + 50);
cout << myTime.GetDateTime().tm_mon << "/" << myTime.GetDateTime().tm_mday << "/" << myTime.GetDateTime().tm_year << endl;
cout << myTime.GetJulianDate() << endl;
- Plot a Matrix of values corresponding to the
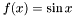 for
for 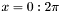 using the Open-Sessame GnuPlot interface.
using the Open-Sessame GnuPlot interface. int stepsize = 0.1;
Matrix datavec(2*M_PI / stepsize,2);
for (int jj = 1; jj <= datavec[MatrixRowsIndex].getIndexBound(); ++jj)
{
datavec(jj,1) = jj * stepsize;
datavec(jj,2) = sin(jj * stepsize);
}
Plot2D(datavec);
- Create a linear interpolation of the
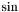 function using a step-size of 0.1
function using a step-size of 0.1 int stepsize = 0.1;
Vector timeVec(2*M_PI / stepsize);
Matrix dataMat(timeVec[MatrixRowsIndex].getIndexBound(), 1);
for (int jj = 1; jj < timeVec[MatrixRowsIndex].getIndexBound(); ++jj)
{
timeVec(jj) = jj * stepsize;
dataMat(jj,1) = sin(jj * stepsize);
}
LinearInterpolator interp(timeVec,dataMat);
Vector chk = interp.Evaluate(0.25);
cout << timevec << endl << datavec << endl << sin(0.25) << " = " << chk << endl;
Attitude Tutorial Answer
- Create an AttitudeState object instance that is initialized to an aligned rotation in the Orbit-Inertial Frame (attitudeframe not yet implemented fully).
AttitudeState myAttState(Rotation(), new AttitudeFrameOI);
- Integrate an attitude for 50 seconds using the following conditions:
First setup the kinematics equation:
static Vector AttituteDynamics(const ssfTime &_time, const Vector& _integratingState, Orbit *_pOrbit, Attitude *_pAttitude, const Matrix &_parameters, const Functor &_forceFunctorPtr)
{
static Vector stateDot(7);
static Matrix bMOI(3,3);
static Matrix qtemp(4,3);
static Matrix Tmoment(3,1);
static Vector qIn(4);
static Vector wIn(3);
qIn = _integratingState(_(VectorIndexBase,VectorIndexBase + 3));
wIn = _integratingState(_(VectorIndexBase + 4,VectorIndexBase + 6));
qIn /= norm2(qIn);
qtemp(_(VectorIndexBase+0,VectorIndexBase+2),_(VectorIndexBase+0,VectorIndexBase+2)) = skew(qIn(_(VectorIndexBase+0,VectorIndexBase+2))) + qIn(VectorIndexBase+3) * eye(3);
qtemp(VectorIndexBase+3, _(VectorIndexBase+0,VectorIndexBase+2)) = -(~qIn(_(VectorIndexBase+0,VectorIndexBase+2)));
qtemp(_,MatrixIndexBase) = 0.5 * qtemp * wIn;
bMOI = _parameters(_(MatrixIndexBase+0,MatrixIndexBase+2),_(MatrixIndexBase+0,MatrixIndexBase+2));
Tmoment = (bMOI.inverse() * (Tmoment - skew(wIn) * (bMOI * wIn)));
stateDot(_(VectorIndexBase,VectorIndexBase + 3)) = qtemp(_,MatrixIndexBase);
stateDot(_(VectorIndexBase + 4,VectorIndexBase + 6)) = Tmoment(_,MatrixIndexBase);
return stateDot;
}
Then setup the driver code to run the above dynamics equation:
RungeKuttaIntegrator myIntegrator;
myIntegrator.SetNumSteps(1000);
vector<ssfTime> integrationTimes;
ssfTime begin(0);
ssfTime end(begin + 50);
integrationTimes.push_back(begin);
integrationTimes.push_back(end);
AttitudeState myAttitudeState;
myAttitudeState.SetRotation(Rotation(Quaternion(0,0,0,1)));
Vector initAngVelVector(3);
initAngVelVector(1) = 0;
initAngVelVector(2) = 0.1;
initAngVelVector(2) = -0.5;
myAttitudeState.SetAngularVelocity(initAngVelVector);
SpecificFunctor AttitudeForcesFunctor(&NullFunctor);
Matrix Parameters = eye(3);
Parameters(1) = 100;
Parameters(2) = 300;
Parameters(3) = 150;
Matrix history = myIntegrator.Integrate(
integrationTimes,
&AttituteDynamics,
myAttitudeState.GetState(),
NULL,
NULL,
Parameters,
AttitudeForcesFunctor
);
- Store the attitude to a text file.
ofstream ofile;
ofile.open("AttitudeHistory.dat");
ofile << history;
ofile.close();
- Plot the attitude history using GnuPlot.
Matrix plotting = history(_,_(MatrixIndexBase,MatrixIndexBase+4));
Plot2D(plotting);
- Store the attitude in DirectionCosineMatrix format in a MatLab file.
Back to: Attitude Tutorials
Orbit Tutorial Answer
Setup the dynamic equations: static Vector TwoBodyDynamics(const ssfTime &_time, const Vector& _integratingState, Orbit *_Orbit, Attitude *_Attitude, const Matrix &_parameters, const Functor &_forceFunctorPtr)
{
static Vector Forces(3);
static Vector Velocity(3);
static Vector stateDot(6);
static AttitudeState tempAttState;
static OrbitState orbState(new PositionVelocity);
orbState.GetStateRepresentation()->SetPositionVelocity(_integratingState);
if(_Attitude)
Forces = _forceFunctorPtr.Call(_time, orbState, _Attitude->GetStateObject());
else
Forces = _forceFunctorPtr.Call(_time, orbState, tempAttState);
Velocity(_) = _integratingState(_(VectorIndexBase+3,VectorIndexBase+5));
stateDot(_(VectorIndexBase, VectorIndexBase+2)) = Velocity(_);
stateDot(_(VectorIndexBase+3, VectorIndexBase+5)) = Forces(_);
return stateDot;
}
Vector OrbitForcesWithDragFunctor(const ssfTime& _pSSFTime, const OrbitState& _pOrbitState, const AttitudeState& _pAttitudeState)
{
Vector Forces;
Vector Position(3); Position(_) = _pOrbitState.GetStateRepresentation()->GetPositionVelocity()(_(VectorIndexBase,VectorIndexBase+2));
double BC = 0.5;
Vector Vrel(3); Vrel = _pOrbitState.GetStateRepresentation()->GetPositionVelocity()(_(VectorIndexBase+3,VectorIndexBase+5));
double Vrel_mag = norm2(Vrel);
Forces = -398600.4418 / pow(norm2(Position),3) * Position;
Forces += -1/2 *1/BC * pow(Vrel_mag,2) * Vrel / Vrel_mag;
return Forces;
}
Finally create the driver program and call the integration:
RungeKuttaIntegrator myIntegrator;
int numOrbits = 2;
int numSteps = 100;
myIntegrator.SetNumSteps(numSteps);
vector<ssfTime> integrationTimes;
ssfTime begin(0);
ssfTime end(begin + 92*60*numOrbits);
integrationTimes.push_back(begin);
integrationTimes.push_back(end);
OrbitState myOrbitState;
myOrbitState.SetStateRepresentation(new PositionVelocity);
myOrbitState.SetOrbitFrame(new OrbitFrameIJK);
Vector initPV(6);
initPV(VectorIndexBase+0) = -5776.6;
initPV(VectorIndexBase+1) = -157;
initPV(VectorIndexBase+2) = 3496.9;
initPV(VectorIndexBase+3) = -2.595;
initPV(VectorIndexBase+4) = -5.651;
initPV(VectorIndexBase+5) = -4.513;
myOrbitState.GetStateRepresentation()->SetPositionVelocity(initPV);
Matrix history = myIntegrator.Integrate(
integrationTimes,
&TwoBodyDynamics,
myOrbit.GetStateRepresentation()->GetPositionVelocity(),
NULL,
NULL,
Parameters,
OrbitForcesFunctor
);
- Store the position and velocity to a text file.
ofstream ofile;
ofile.open("OrbitHistory.dat");
ofile << history;
ofile.close();
- Plot the orbit position vector using GnuPlot.
Matrix orbitHistory = myOrbit->GetHistory().GetHistory();
Matrix orbitPlotting = orbitHistory(_,_(2,4));
Plot3D(orbitPlotting);
[ time, r1, r2, r3, v1, v2, v3]
[ 5400, -5386.654, 562.845, 4034.074, -3.518027, -5.617977, -3.890888 ]
- Store the orbit Keplerian parameters in a MatLab file.
Back to: Orbit Tutorials
Coupled Tutorial Answers
- Create an Environment object of the Earth using the above (Orbit & Attitude) disturbance force & torque functions.
- Create a Propagator that will propagate the above Orbit & Attitude objects and using the Environment object.
- Use a linear interpolator for the OrbitHistory.
- Use loose coupling (orbit independent of attitude, but attitude dependent on position).
- Propagate the orbit and attitude for 2 orbits.
- Plot the position and attitude using gnuplot.
- Propagate another 2 orbits.
- Add the new states to the previously made plots.
Back to: Coupled Attitude & Orbit Tutorials
Generated on Wed Aug 6 12:59:10 2003 for Open-Sessame Framework by
 1.3
1.3
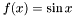 for
for 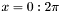 using the Open-Sessame GnuPlot interface.
using the Open-Sessame GnuPlot interface. 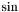 function using a step-size of 0.1
function using a step-size of 0.1  1.3
1.3