Gravity force function modeling two-body gravity.
Newton formulated the simplified two-body equation, or Law of Universal Gravitation. This formulation is a simplified model because it only accounts for two bodies: the central body, and the spacecraft. In general it can be applied to any two massive bodies which have a gravitational attraction with the following assumptions:
- The bodies are spherically symmetric.
- There are no external or internal forces acting on the system other than the gravitational forces which act along the line joining the centers of the two bodies.
- Newton's Law of Universal Gravitation states that the force of gravity between two bodies is proportional to the product of their masses and inversely proportional to the square of the distance between them:
where
is the force of gravity acting on mass 
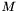and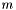 
, and the vector between the two masses is 
. The parameter 
is the universal contant, which is usually measured by observing the quantity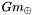 
, since the mass of the earth is large and more easily measured. This gravitational parameter, 
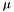has a modern (most recent, accurate) value of 
. It is important to note that the vector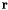 
is measured with respect to inertial axes.
- Parameters:
-
_currentTime current simulation time _currentOrbitState current orbit state, including representation and reference frame _currentAttitudeState current attitude state, including rotation and reference frame _parameterList EnvFuncParamaterType parameter list for external variables = [ 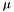], gravitational parameter [km^3/(solar s)^2]
- Returns:
- This force functions returns a 3-element vector of forces (x,y,z) due to gravity using a two-body simplified force model.
- Examples:
- testEnvironment.cpp, and testPropagation.cpp.
Definition at line 47 of file GravityFunctions.h.
], Ballistic Coefficient, atmospheric density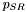 
, or change in momentum, is the main parameter in determing the force of the solar-radiation pressure. For the Earth, this has a nominal value of 
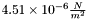, where more precise values can be calculated depending on the time of year, as well as position from the Sun. The effect of solar-radiation pressure also varies due to the reflectivity, 
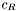, of the spacecraft, where 0.0 indicates no effect, 1.0 is a completely absorbing body, and 2.0 is an absorbing and reflecting body.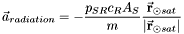
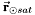is the distance from the satellite to the sun (or light-emitting body), and 
is the spacecraft's exposed area to the sun. This value of area is very important for calculating the disturbance difference as the spacecraft passes from full sunlight, into eclipse, or when being shadowed by another body (moon or another spacecraft).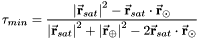
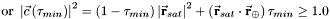
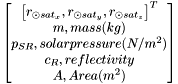
= distance from satellite to the sun (m) 