Attitude Dynamics equation using Quaternions and Angular Velocities as the state variables.
The rotation of a rigid body is described by the kinematic equations of motion and the kinetic equations of motion. As discussed above, the kinematics specifically model the current attitude of the body with respect to time. The dynamics are characterized by the absolute angular velocity vector, $$.
Each attitude representation has a set of equations that describe its time rate of change due to the dynamics of the rigid body.
The propagation of the Quaternion kinematics is defined as:
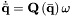
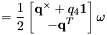
- The differential equations for the angular velocity in the body frame are based on Euler's equation:
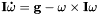
where
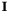is the spacecraft moment of inertia matrix, 
is the body angular velocity, and 
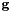are the spacecraft torques.
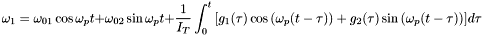
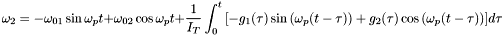
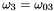
- Parameters:
-
_time current time (in seconds) _state vector of states,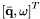 
(-, radians/second) _pOrbit pointer to the current Orbit instance _pAttitude pointer to the current Attitude instance _parameters additional parameters for integration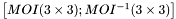 
_torqueFuncPtr pointer to the torque calculating function
- Returns:
- This attitude dynamics RHS returns the 7-element vector of time derivatives of state
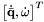
Definition at line 93 of file QuaternionAngVelDynamics.h.
